Duyệt vét cạn (brute force) là phương pháp tìm kiếm tất cả các lời giải có thể của một vấn đề bằng cách duyệt qua tất cả các khả năng. Tuy nhiên, do phải duyệt qua tất cả các khả năng, thời gian thực hiện của phương pháp này thường rất lâu, đặc biệt là với các bài toán có không gian tìm kiếm lớn.
Backtracking là một phương pháp cải tiến của duyệt vét cạn. Thay vì thử tất cả các khả năng, backtracking sẽ thử từng bước, và nếu một bước nào đó không khả thi, nó sẽ quay lui (backtrack) và thử bước tiếp theo. Kỹ thuật này giúp giảm số lượng các bước cần thử, nhưng với các bài toán phức tạp, vẫn có thể dẫn đến việc thử nhiều lần các bước tương tự nhau.
Kỹ thuật memoization là một phương pháp tối ưu hóa trong lập trình, giúp giảm thời gian thực hiện của các thuật toán đệ quy bằng cách lưu trữ kết quả của các bài toán con đã được tính toán trước đó. Khi gặp lại một bài toán con đã được xử lý, thay vì tính lại, chúng ta chỉ cần lấy kết quả đã lưu từ bộ nhớ, giúp tiết kiệm thời gian và tài nguyên.
Để hiểu hơn về thuật toán này hãy cùng phân tích 1 bài toán ví dụ.
Cho một lưới 𝑚×𝑛 với các ô chứa các giá trị dương, hãy tìm đường đi ngắn nhất từ ô trên cùng bên trái (0, 0) đến ô dưới cùng bên phải (m-1, n-1), sao cho tổng các giá trị trên đường đi là nhỏ nhất. Bạn chỉ có thể di chuyển xuống dưới hoặc sang phải.

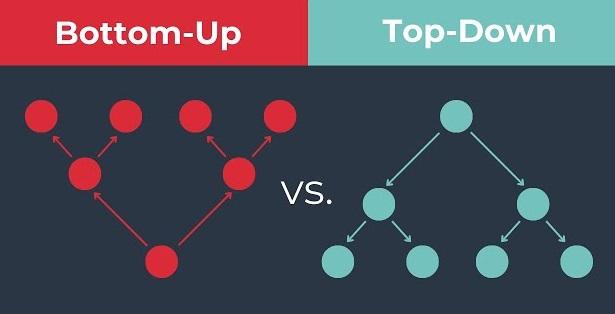
Trong cách tiếp cận bottom-up, chúng ta xây dựng bảng kết quả từ dưới lên trên. Chúng ta khởi đầu từ ô cuối cùng và tính toán ngược lên ô đầu tiên bằng cách sử dụng một mảng hai chiều để lưu trữ kết quả tạm thời. Cách tiếp cận này thường được sử dụng trong lập trình động (dynamic programming).
Trong cách tiếp cận top-down, chúng ta bắt đầu từ ô đầu tiên và sử dụng đệ quy để giải quyết bài toán bằng cách chia nhỏ nó thành các bài toán con. Kỹ thuật memoization được sử dụng để lưu trữ kết quả của các bài toán con đã tính toán, giúp tránh việc tính toán lại.
Chúng ta sẽ sử dụng đệ quy và memoization để giải quyết bài toán này. Mỗi khi chúng ta tính toán đường đi ngắn nhất từ một ô cụ thể đến đích, chúng ta sẽ lưu kết quả vào bộ nhớ. Khi gặp lại ô này, chúng ta chỉ cần lấy kết quả từ bộ nhớ ra thay vì tính lại.